我们的欧几里得辅导课程配有独家自研教材,授课老师均为海内外名校毕业,具有丰富的竞赛教学经验,并根据不同基础学生开设了不同的班课,真正做到有的放矢,事半功倍!

最新课程安排

扫码试听课程,了解更多课程详情!

Euclid欧几里得冲刺班
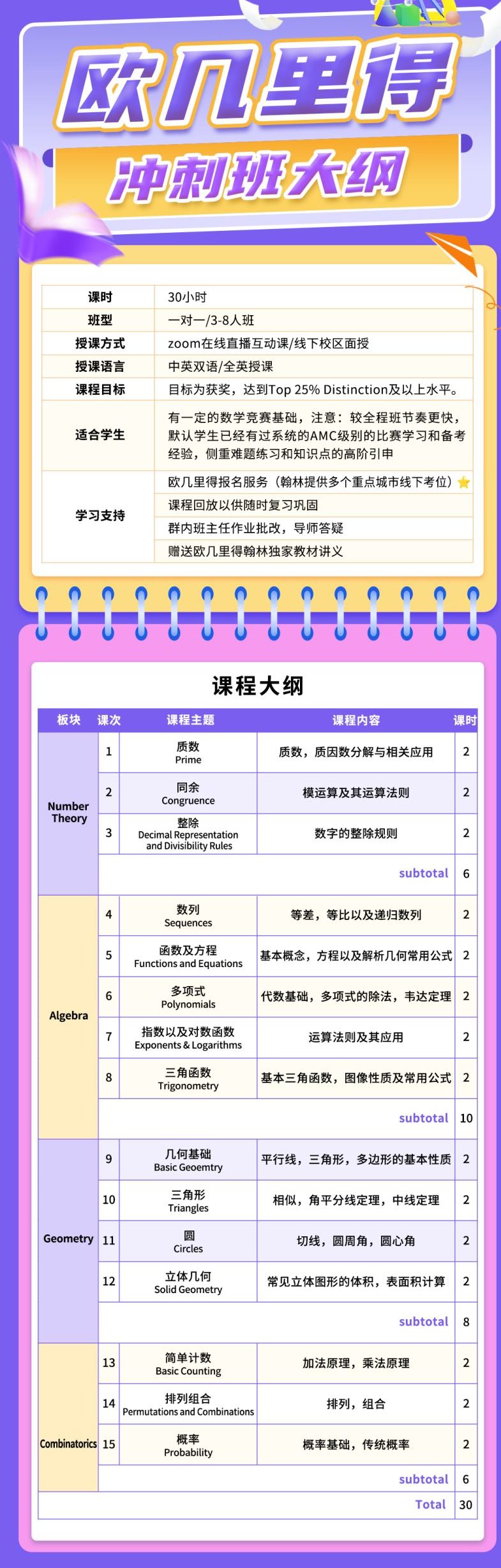
| 班型 | 人数 | 课时 | 开课时间 |
| 冲刺班 | 1v1/3-8人 | 30h | 详询老师 |
| 全程班 | 1v1/3-8人 | 40h | 详询老师 |
扫码试听课程,了解更多课程详情!

导师阵容
Z老师
美国罗切斯特大学理论数学博士
复旦大学上海数学中心博士后研究员
初中阶段获得全国初中数学联赛一等奖、化学联赛二等奖并保送重庆南开中学理科竞赛实验班。
高一获得重庆市数学竞赛一等奖,全市第三名。高三获得全国高中数学联赛一等奖,生物联赛二等奖。
7年理论数学的研究和相关教学经验,曾系统教授过大学数学系本科至研究生大部分专业课程。
读博期间曾参与了大量AMC与美国大学生数学竞赛(Putnam、Virginia Tech等)的讲座与培训工作。
辅导战绩:
2021年11月AMC学员最高分150分(满分),AIME 10分以上学员4位,7分以上学员12位,5名学员达到USA(J)MO分数线。
2022Euclid(欧几里得数学竞赛)辅导四名学生分别获得91分、90分、88分、87分。
G老师
北京大学硕士毕业
曾获全国大学生数学建模竞赛一等奖;全国高中数学联赛二等奖,全国希望杯数学竞赛三等奖。
辅导战绩:
美国AMC12/10/8竞赛学生进复赛以及获奖率超过65%,AMC12最高分150,140+的不少,AMC10最高分144;比如2022年17个学生晋级AIME,4个拿下1%;2023年二十几个学生晋级AIME,基本都是前5%或1%;欧几里得竞赛学生获奖(前25%)率75%左右,最高分94;澳大利亚AMC竞赛学生也取得了靠前的奖项;
ALEVEL学生A以及A*率96%以上,高数有学生FP1 FM FP2三门离满分差1分;AP微积分学生5分率95%;IB学生提分很快,目前IB HL学生基本都提到7分,SL曾有学生从1-2分提到5-6分用了3个月左右。
学员战绩
🏆 2025年
233位学员Distinction
8人90+分, 97人80+分
🏆 2024年
177位学员Distinction
17人90+分, 75人80+分
🏆 2023年
165位学员Distinction,参考学员获奖率70%;
8 人90+分, 63 人80+分
🏆 2022年
96位学员Distinction,参考学员获奖率75%;
分数线68分,学员7人90-93分,16人85-89分,26人80-84分,47人68-79分。
🏆 2021年
33位学员Distinction,参考学员获奖率50%;
4人90分以上(94、93*2、90),12人80分以上。
欧几里得数学竞赛辅导课程
适合人群:12年级及以下年级学生。
课程描述:
欧几里得数学竞赛辅导课程,是一门针对初、高中生的数学竞赛辅导课程。本课程涵盖了欧几里得数学竞赛的各个方面,包括数学推理、几何证明和解题技巧等,旨在帮助学生提高数学素养、拓展数学思维、增强数学能力。不论是初学者或者是有经验的竞赛选手都可以在我们的课程中找到适合自己的内容。师资团队由经验丰富、教学能力卓越的数学竞赛老师组成,为学生提供个性化教学,真正做到因材施教。
课程大纲
(Materials with * are aimed for the potential last Problems)
Number Theory
(1)Prime factorization
——Number of factors, Sum/Product of factors
——LCM and GCD, *Euclidean Algorithm and Bézout's Theorem
(2)Congruence and Modular Algebra
——Principles of Modular Calculations
——*Euler’s Theorem/Fermat's Little Theorem
——*Chinese Remainder Theorem(CRT)
(3)Digits and Base-n Representation
——Mutual Conversion between different bases
(4)Diphantine Equations
——Estimation and Molular Method
Algebra
(1)Sequences
——Arithemetic and Geometric Sequences
——Periodic Sequences, *Recursive Sequences and Characteristic Equation Method
——*Conjecture and Mathematical Induction Proof
(2)Functions and Equations
——Elementary Functions (Linear, Quadratic, Exponential, Logarithmic, Trigonometric) and their properties
——Functional Equations
——*Gaussian/Floor function
(3)Inequalities and Extreme Value Problems
——Simple Polynomial Inequalities
——AM-GM Inequality, *Cauchy inequality
(4)Polynomials
——Division Algorithm of Polynomials and the Remainder's Theorem
——Fundamental Theorem of Algebra (Polynomial Factorization) and Vieta's Theorem
——The Rational Root Theorem
Geometry
(1)Triangles and Polygons
——The Law of Sines, The Law of Cosines
——Area Method and Heron's formula
——*Menelaus's theorem, Ceva's theorem, Stewart Theorem
——Centers of triangle
(2)Circles
——Chords, Arcs, Tangents, Inscribed and Central accepted angles
——Cyclic Quadrilateral
——Power of a Point Theorem, *Ptolemy's theorem
(3)Basic Coordinate Geometry
——Coordinate System and Equations of lines, Circles
(4)Basic Solid Geometry
——Lines in space, Planes; Rectangular Box, Pyramids, Prisms, Sphere and Cones,Frustums
Combinatorics
(1)Basic Counting Principle
——Sum Rules and Product Rules
(2)Permutations and combinations
——Combinatorics numbers and *Combinatorics identities
——Grouping Theorems, Boards Method and the Problem of Balls into Boxes
(3)Logic reasoning
——*Pigeonhole principle
扫码了解课程详情,试听名师课程
领取课程优惠+一对一学术规划!


